Post #441339

Небоскребы

Головоломка «Небоскребы» («Skyscrapers») довольно широко распространена как в сети, так и в различных мобильных приложениях. Ее цель — заполнить числами квадратное поле размером чаще всего 4х4, 5х5 или 6х6 клеток. Реже встречаются задачи на полях размером 7х7 и больше. Правила игры весьма просты, а решение бывает очень увлекательным.
Числа от 1 до размера квадрата представляют собой высоту здания, расположенного в этой клетке, и в каждом ряду и столбце числа не должны повторяться. Вдоль периметра квадрата расположены ключи — числа, с помощью которых зашифровано расположение зданий в клетках. Каждое число показывает, сколько зданий можно увидеть, если посмотреть на поле с этой стороны. Например, если посмотреть на ряд 3-1-6-5-2-4 слева, то мы увидим два здания, 3 и 6, а если справа, то три — 4, 5 и 6. Вот и все правила.
Рассмотрим это на примере простой головоломки.

Размер этой головоломки - 5х5, значит, в ней должны располагаться здания высотой от 1 до 5 этажей. Решение обычно начинается с самых удобных ключей - это единица и число, равное размеру квадрата, в данном случае 1 и 5. Если рядом с полем стоит ключ 1, значит, от него видно только одно здание. Это возможно только тогда, когда в ближней к нему клетке стоит самое высокое здание. Если же ключ равен 5, значит, с его стороны видно все пять зданий, и это возможно только в том случае, когда здания расположены в возрастающем порядке 1-2-3-4-5. Проставим пятерки там, где имеем ключ 1.

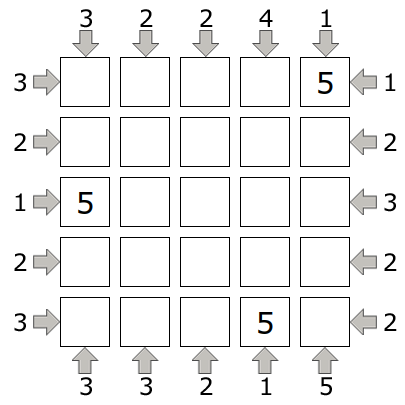
Пока что нам неизвестно расположение пятерок во 2-й и 3-й вертикали (при отсчете слева направо). Но обратим внимание, что под 2-й вертикалью стоит ключ 3. А это значит, что если пятерка стоит в первой или второй клетке от ключа, то 3 здания мы никак с этой стороны не увидим - пятерка закроет все остальные здания. То есть 5 может стоят только начиная с третьей клетки и дальше. Но в третьей и пятой горизонтали пятерки уже стоят, и у нас остается только одно возможное место - в 4-й клетке. Тогда и в третьей вертикали остается только одно возможное для пятерки место.

Под 5-й вертикалью видим ключ 5, значит, в этой вертикали можно проставить все цифры по порядку.

Рассмотрим 2-ю горизонталь *-*-5-*-2, справа от нее стоит ключ 2. И это возможно только, если между 5 и 2 стоит 1. Ведь если там поставить 3 или 4, то справа мы увидим 3 здания, а не 2. Слева от этой горизонтали также стоит ключ 2, значит сначала должна стоять 4, а потом 3 (в противном случае опять же увидим три здания).

Над 4-й вертикалью стоит ключ 4. Оставшиеся в этой вертикали здания можно расположить только одним способом так, чтобы было видно 4 здания.

Подумаем, где можно поставить четверку в нижнем ряду. Для нее осталось только два возможных места - вторая и третья клетка. Но если поставить ее во второй клетке, то снизу во 2-й вертикали мы увидим 2 здания, а должно быть 3. То есть четверка может стоять только в третьей клетке. Теперь и во второй вертикали для четверки остается только одно возможное место.

Теперь легко заполняются оставшиеся клетки во 2-й вертикали, а затем и все остальные клетки поля. Задача решена.

Следует отметить, что рассмотренный уровень - один из самых простых. Очень часто в таких задачах даются далеко не все ключи, но этого оказывается достаточно для того, чтобы найти единственное решение. Сложность небоскребов бывает очень разная, но должен честно признаться, что задачи уровня "extreme" и тем более "insane" (экстремально и безумно сложные) я решать не смог. Логике они не поддаются, там только надо перебирать варианты.
Предлагаю вам решить задачу средней сложности. Ответ на нее (а возможно, и разбор) будет позже.